Сравнительный анализ методики ознакомления сравенствами

Для того, чтобы найти способ решения уравнения, достаточно определить сначала по схеме, а позже и сразу по формуле, чем является неизвестная величина: частью или целым. Если известная величина является целым, то для ее нахождения нужно сложить, а если она часть, то из целого нужно вычесть известные части. Таким образом, ребенку не нужно запоминать правила нахождения неизвестного слагаемого, уменьшаемого и вычитаемого.

Успешность ребенка, его навык при решении уравнений будут зависеть от того, может ли ребенок переходить от описания отношения между величинами с помощью схемы к описанию с помощью формулы и наоборот. Именно этот переход от уравнения как одного из вида формул к схеме и определения с помощью схемы характера (часть или целое) неизвестной величины являются теми основными умениями, которые дают возможность решать любые уравнения, содержащие действия сложения и вычитания. Другими словами, дети должны понять, что для правильного выбора способа решения уравнения, а значит, и задачи нужно уметь видеть отношение целого и частей в чем и поможет схема. Схема здесь выступает в качестве средства решения уравнения, а уравнение, в свою очередь, как средство решения задачи. Поэтому большинство заданий ориентировано на составление уравнений по заданной схеме и на решение текстовых задач путем составления схемы и с ее помощью составления уравнения, позволяющего найти решение задачи.

Традиционная школа.

Изучение уравнений в начальных классах традиционной школы происходит в несколько этапов. Программой традиционной школы предусмотрено знакомство детей с уравнениями первой степени с одной неизвестной. Большое значение в плане подготовки к введению уравнений имеют упражнения на подбор пропущенного числа в равенствах, деформированных примерах, вида 4+€=5, 4–€=2, €–7=3, и т.п. в процессе выполнения таких упражнений дети привыкают к мысли, что неизвестным может быть не только сумма или разность, но и одно из слагаемых (уменьшаемое или вычитаемое). До 2 класса неизвестное число обозначается, как правило, так: €, ?, *. Теперь же для обозначения неизвестного числа используют буквы латинского алфавита. Равенство вида 4 + х = 5 называют уравнением. Равенство, где есть буква, называют уравнением.

На первом этапе уравнения решают на основе состава числа. Учитель знакомит с понятием неизвестного, понятием уравнение, показывает разные формы чтения, учит записывать уравнения по диктовку, разбирает понятия “решить уравнение”, “что называется корнем”, “что есть решение уравнения”, учит проверять решенные уравнения.

На втором этапе решение уравнений происходит с использованием зависимости между компонентами. В этом случае при нахождении неизвестного числа можно пользоваться приемом замены данного уравнения равнозначным ему уравнением. Опорой перехода может быть граф. Приведу примеры уравнений и замены их равнозначными уравнениями с опорой на графы.

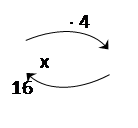х × 4 = 16

х = 16 : 4

х = 4

4 × 4 = 16

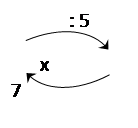х : 5 = 7

х = 7 × 5

х = 35

35 : 5 = 7

После того как учащиеся научатся решать простейшие уравнения, включаются более сложные уравнения видов: 48 – х = 16 + 9, а – (60 – 14) = 27, 51 – (х + 15) = 20, решение которых выполняется также на основе взаимосвязи между результатами и компонентами арифметических действий, ведется подготовка к решению задач способом составления уравнений. Для решения таких уравнений необходимы знания порядка действий в выражении, а также умения выполнять простейшие преобразования выражений. Уравнения указанных видов вводятся постепенно. Сначала простейшие уравнения усложняются тем, что их правая часть задается не числом, а выражением. Далее включаются уравнения, в которых известный компонент задан выражением. Полезно учить читать эти уравнения с названием компонентов. Наконец, приступают к решению таких уравнений, где один из компонентов является выражением, включающим неизвестное число, например: 60 – (х + 7) = 25, (12 – х) + 10 = 18.

При решении уравнений такого вида приходится использовать дважды правила нахождения неизвестных компонентов. Рассмотрим.

Обучение решению таких уравнений требует длительных упражнений в анализе выражений и хорошего знания правил нахождения неизвестных компонентов. На первых порах полезны упражнения в пояснении решенных уравнений. Кроме того, следует чаще решать такие уравнения с предварительным выяснением, что неизвестно и какие правила надо вспомнить, чтобы решить данное уравнение. Такая работа предупреждает ошибки и способствует овладению умением решать уравнения.