Понятия функции и графика

Таким образом, для построения графика функции следует построить график функции и увеличить его ординаты в раз при (растянуть график от оси абсцисс с коэффициентом ) или уменьшить его ординаты в раз при (сжать график к оси абсцисс с коэффициентом ) (рис. 7).

Рассмотрим функцию . Очевидно, что при всех значениях аргумента ординаты графика функции равны по абсолютной величине, но противоположны по знаку ординатам графика функции . Поэтому для построения графика функции следует построить график функции и отразить его симметрично относительно оси абсцисс (рис. 8).

Соединяя предыдущие рассуждения с последним правилом, можно строить график функции для значения любого знака.

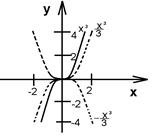После изложения теоретического материала учитель разбирает пример: выделяет шаги преобразований и строит график.

Пример. Построить график функции .

1) Строим график функции ;

Рис. 9

2) сжимаем график к оси абсцисс с коэффициентом ;

3) отображаем график симметрично относительно оси абсцисс.

Последний полученный график есть график функции (рис. 9).

Закрепление полученных знаний

Учащиеся объединяются в пары и решают задания. После выполнения задания, вызвавшие затруднения, разбираются на доске с подробным решением. Во время разбора учитель акцентирует внимание учащихся на более сложных моментах.

1. Построить графики функций.

1) ; 2) ; 3) ; 4) ; 5) .

2. Для развития творческой активности и осознанного понимания материала учитель предлагает составить каждой паре учащихся по одному заданию (составить функцию и построить ее график) на практическое применение изученного материала. Затем некоторые из заданий, наиболее трудные, разбираются учащимися при помощи учителя.

Подведение итогов занятия

- Какое преобразование Вы использовали для построения графиков функций?

- Сформулируйте суть изученного преобразования.

-Оцените свою работу на занятии по 5-ти бальной системе и поставьте соответствующую оценку в индивидуальную карточку результатов деятельности.

Постановка домашнего задания

Повторить теоретический материал и выполнить письменно задания.

1. Построить графики функций.

1) ;2) ;3) ;4) ;5) .