Понятия функции и графика

Ординаты графика суммы функций получаются путем сложения ординат графиков складываемых функций для каждого значения аргумента (для каждой абсциссы) из области определения суммы.

Рис. 14

Другими словами, чтобы построить график функции , нужно построить графики функций и в одной и той же системе координат, а затем в каждой точке к отрезку, изображающему ординату первого графика, пристроить отрезок, изображающий ординату второго графика, при этом второй отрезок откладывать вверх, если , и вниз, если (рис. 14).

Аналогично определяется разность двух функций и строится ее график. При построении графика разности можно поступить иначе: построить графики функций и , затем график функции отобразить симметрично относительно оси Ох, тем самым получится график функции , и, наконец, складываются графики функций и .

Закрепление полученных знаний

Учитель рассматривает на конкретном примере, как производится сложение функций, и строит график полученной функции.

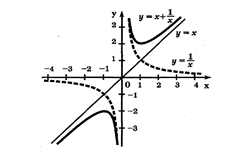Пример. Построить график функции .

1) Строим графики функций и ;

Рис. 15

2) для каждого значения (0) складываем соответствующие отрезки, изображающие ординаты.

Получаем искомый график (рис. 15).

Практические задания учащиеся выполняют индивидуально с последующим разбором на доске.

1. Сравните значения и , где , , при .

2. Построить графики функций.

1) ; 2) ; 3) ; 4) .

Подведение итогов занятия

- Какую тему мы изучили сегодня на занятии?

- При каком условии может осуществляться арифметическое действие (сложение или вычитание) над функциями?

Постановка домашнего задания

Повторить теоретический материал.

Построить графики функций.

1) ;2) ;3) ; 4) .